0、引子
作为一名同时热爱数学和计算机的极客来说,不玩玩分形是不可能的。 本篇博文(博客文章简称)对分形几何仅是浅尝辄止,关于高级作法及变形将会在以后的文中介绍。
1、分形
概括地说,具有某种自相似性质的点集就是分形。分形曾被认为是几何中的怪胎,后来建立了分形维数(即非整数阶维数或豪斯多夫维数)的概念,我们才更深刻地认识了它。 在经典几何中,分形的典型例子有:康托尔集、谢尔宾斯基三角形和地毯、门格海绵、龙形曲线、空间填充曲线和科赫曲线。这些例子的共性就是它们可以由某种迭代变换产生。它们简洁而又形象,但是却不利于建立解析模型,而利用复变知识则可以改善这一点。 在复分析中,可以通过非常简单的迭代来生成分形。比如朱利亚集($J$)就是通过变换${{f}_{c}}\left( z \right)={{z}^{2}}+c$产生的。实际上,对于给定的复数$c$来说,可以将朱利亚集表示为:
\[J=\left\{ z\ |\ \ \underset{n\to \infty }{\mathop{\sup }}\,\left| f_{c}^{n}\left( z \right) \right|<+\infty ,\ z\in \mathbb{C} \right\}\]
,其中$f_{c}^{n}\left( z \right)={{f}_{c}}\left( f_{c}^{n-1}\left( z \right) \right)$。一个与朱利亚集关系密切的集合——曼德博集($M$),定义与朱利亚集非常相似:
\[M=\left\{ c\ |\ \ \underset{n\to \infty }{\mathop{\sup }}\,\left| f_{c}^{n}\left( 0 \right) \right|<+\infty ,\ c\in \mathbb{C} \right\}\]
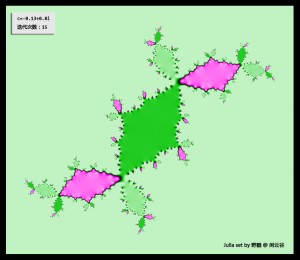
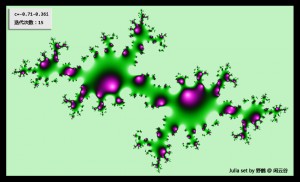
。同时,它们之前也有深刻的联系,比如,只有当$c\in M$时,$J$才非空。 上面的介绍,实际上恰好给计算机绘制分形图案提供了一个方法——将复平面上的点按发散或收敛速度定义颜色。构造分形有四种常见的方法,逃逸时间分形、迭代函数系统、随机分形、奇异吸引子。这里介绍的方法属于逃逸时间分形方法。下面是一些朱利亚集的一些例子。
2、数学+计算机→艺术
2.1、找到合适的$c$及本色方案
说明:下面的动态演示,需要您的电脑上安装Mathematica或CDF Player。
您可以通过按小球来给$c$赋值,也选择迭代次数或本色方案。
这样您可以快速找出想的$c$以及其它参数
点此查看CDF动态演示 >>
2.2、绘图代码
c = -0.13 - 0.81 I;
x0 = 1.4;(*定义水平宽度的一半*)
y0 = 1.3;(*定义垂直高度的一半*)
st = 0.01;(*定义步长*)
fg1[z_, c_] := Module[{z0 = z^2 + c, dt = (1 + Sqrt[1 + 4 Abs[c]])/2},
For[k = 1, k <= 15, k++,
If[Abs[z0] > dt, z0 = 1; Break[];, z0 = z0^2 + c;]; ];
If[Abs[z0] > 1, 1, Abs[z0]]
]; (*定义迭代函数*)
ArrayPlot[Table[fg1[x + I y, c], {y, -y0, y0, st}, {x, -x0, x0, st}], ImageSize -> Floor[2 x0/st], Frame -> None, ColorFunction -> "Rainbow"](*绘图*)












from: 分形2之无穷迭代 | 闲云谷 - 数理版