之前写过一篇平滑手画线的短文,只适用于简单封闭曲线的情形,很多朋友感兴趣。于是再写一篇,算是自答上一篇留下的问题吧。
这次使用的方法我也叫不上名字来,只是在地铁上忽然想起来的。适用于一笔画形成的曲线,可以有交叉也可以不封闭。其实,解决问题的核心部分就是将曲线上的点按一笔画的顺序排序。大体方法如下:
- 在曲线上选择一个初始点作为当前位置。
- 任意选择一个初始方向作为记忆方向。
- 以当前位置为中心截取图像局部。
- 在上一步截取的局部曲线上寻找一点,使得当前位置到此点的向量与记忆方向的夹角最小,并将此点作为新的当前位置。
- 判断是否遍历曲线。是:退出,否:转到第3步。
对于封闭的一笔画,上面的方法可以直接运用。对于非封闭的一笔画,需要在第1步时,选择一笔画的下笔或离笔处作为当前位置才可以遍历曲线。
例一:封闭有交叉的一笔画曲线
原图
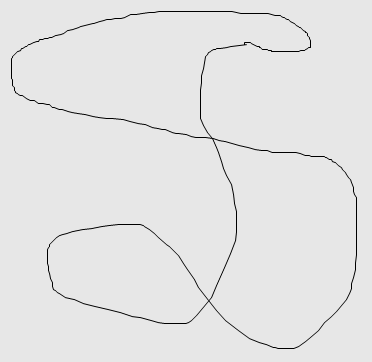
处理后

处理过程
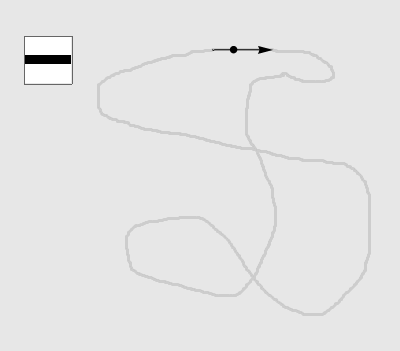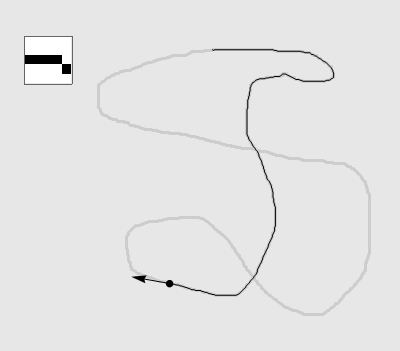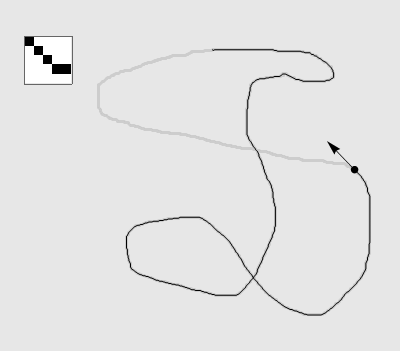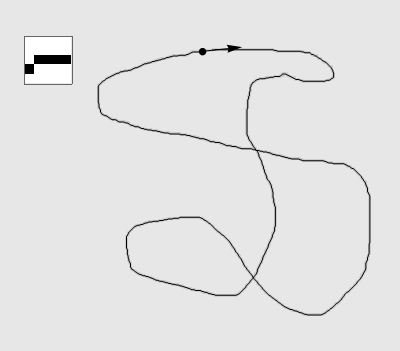
注:左上角图例为实时局部,图中圆点为当前位置,箭头为记忆方向(未展示模长)。
例二:非封闭有交叉的一笔画曲线
下面的一笔画,是父亲在我很小的时候教我画的,大概已经过去20年了,依然记得,但却明显没小时候画的好了!
原图

处理后

处理过程

Mathematica代码
准备数据
下面代码中的graph请先赋值为待处理图像,推荐方法:
在Mathematica中打开绘图工具(Graphics>Drawing Tools),新建(Operations>New),自由手绘线(Tools>Freehand Line)。详见下图:

gM = ImageData[Thinning[ColorNegate@Binarize[graph]]];(*图像矩阵*)
pts = Union[Position[gM, x_ /; x > 0.5]];(*点的矩阵坐标*)
mc[m_, {r_, c_}, y_] :=
m[[r - y ;; r + y, c - y ;; c + y]];(*抓取矩阵m的局部,以r行c列为中心,向外扩展y层*)
order = Ordering[
Total[mc[gM, #, 10], 2] & /@ pts];(*对于非封闭曲线,选取曲线的首尾坐标。这里的10可适当调整*)
rcB = pts[[order[[1]]]];(*首-坐标*)
rcE = pts[[order[[2]]]];(*尾-坐标*)
rc = rcB;(*行列坐标*)
rcs = {rcB};(*行列坐标集*)
\[Lambda] = 0.75;(*记忆系数*)
rcPLast = {1, 1};(*上次移动向量,有记忆功能,记忆系数\[Lambda]越大,记忆越强。也可理解为惯性*)
点的排序
rcP = Complement[
Position[mc[gM, rc, 2], x_ /; x == 1], {{2, 2}, {2, 2} - rcP}][[
1]] - 2;(*移动向量*)
AppendTo[rcs, rc = rc + rcP];
rcPLast = (1 - \[Lambda]) rcP + \[Lambda] rcPLast;
While[True,
rcP = Complement[
Position[mc[gM, rc, 2],
x_ /; x == 1], {{3, 3}, {3, 3} - rcP, {3, 3} -
Total[Differences[rcs[[-Min[3, Length[rcs]] ;;]]]]}] -
3;(*可能的移动向量,用Complement删掉最近两次走过的坐标*)
If[Length[rcP] <
1 || (Length[rcs] >= Length[pts]/2 &&
Min[Norm[rc - rcB], Norm[rc - rcE]] < 3), Break[]];(*退出条件*)
If[Length[rcP] > 1,
rcP = rcP[[(Ordering[rcPLast.#/Norm[#] & /@ rcP])[[-1]]]],
rcP = rcP[[1]]];(*退出条件*)
AppendTo[rcs, rc = rc + rcP];
rcPLast = (1 - \[Lambda]) rcP + \[Lambda] rcPLast;
]
平滑
Rotate[Graphics[{BSplineCurve[rcs[[1 ;; -1 ;; 15]],
SplineClosed -> (Norm[rcs[[1]] - rcs[[-1]]] < 6)]}], -Pi/2]
此处未注重平滑算法,实际上在点排序过程中的记忆向量是可以加以利用的。比如在记忆向量变化较大的拐角处应该抓取更多的关键点,在记忆向量变化较小处可以抓取较少的关键,再进行绘图,会得到更好的效果。
其它可用函数
PixelValuePositions(*获取图像中指定相互的坐标,左下角为{1,1}。本文没有使用此函数,是由于对于ImageData得到的矩阵中左上角坐标是{1,1}。*)
FindShortestTour(*查找最短路径。在本问题中,对于交叉图的处理往往得到不想要的结果:把交叉点处理为非交叉*)
LowpassFilter(*低通滤波器。将数据中的高频信息滤掉,在本例中,手的抖动相对于光滑的曲线来说就是高频部分。*)
对于查找最短路径函数 FindShortestTour 来说,是解决此问题的又一捷径(欲穷千里目,更上一层楼。如果身边有楼就没有必要自己修建,如果不够高或人家不让上,自己建也未尝不可,只是要考虑一下时间成本)。对于本问题,此函数的不足之处在于处理交叉点上,如果可以接受就直接使用之。
滤波器是信号处理中最常用的工具,各种非常简单的滤波器的组合往往能达到意想不到的效果。Mathematica中的 LowpassFilter 函数,除信号输入外,还有一个必选参数(截断频率,即干掉高于此频率的信号)和两个可选参数(滤波器的核的长度,根据图像大小和复杂度选取;还有窗函数,对于手绘线来说主要是由于手抖动产生的随机波动,对主线影响不大,个人感觉使用狄利克雷窗函数就行)。
程序下载
http://pan.baidu.com/s/1o74TORg



这个吊。。
漂亮!
期待背单词工具!
这个估计要往后推了,最近要学一下通信原理。
野鹤 你不是在360工作吗 怎么又学通信原理呢 莫非想跳槽了?<- _ <-
有可能明天考个博士
明天还是高考呢~~ <- _ <- 不知不觉胡混了几年
你参加今年高考啊,还有如此闲心,看来志在必得了。
祝金榜题名!
应该说离开高考几年了
哦,那是我理解错了。